【筆記】資料結構與演算法 (JavaScript) (2) - Sliding Window & Recursion

這篇是接著「資料結構與演算法 (JavaScript)（1）」所撰寫的第二篇，一樣是資料結構與演算法 (JavaScript) 的課程筆記，這篇著重在 Sliding Window 與 Recursion 這兩種演算法，相關的例題都是課程裡的提供的練習，接著進入正題溜～

Sliding Window (滑動視窗法)

不太確定這個演算法的中文怎麼稱呼才好， Sliding Window 演算法是非常廣泛運用的演算法，這個名字最早是從滑動視窗協議（Sliding Window Protocol）而來的，這個協議被運用在網路傳輸的流量控制，避免傳輸上的壅塞。

說到 Sliding Window 我腦中就浮現國中地科的圓形星座盤，哈哈哈這樣有感覺嗎？
沒有的話繼續往下看看張圖，就是 Sliding Window 的運算邏輯：

Image Source: Sliding Window Algorithm

Sliding Window 用在演算法上其實就如其名，在做搜索和運算時只針對固定的區間（視窗）做計算，再將該視窗移動，並做相同的搜索與迭代計算目標，通常出現在計算陣列與字串的問題。

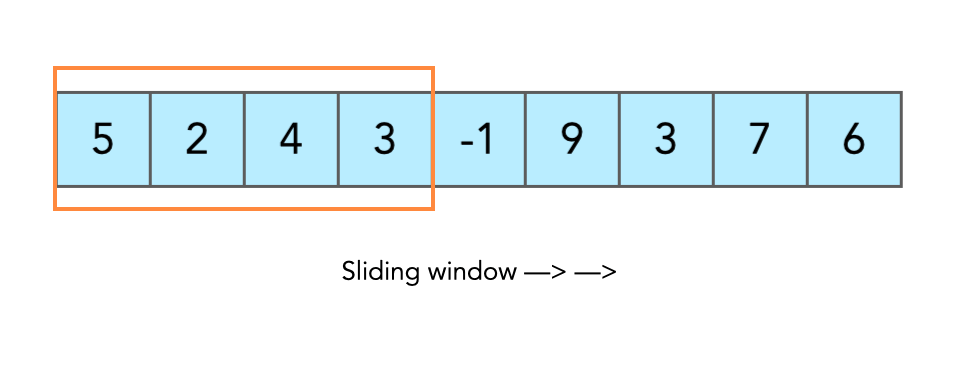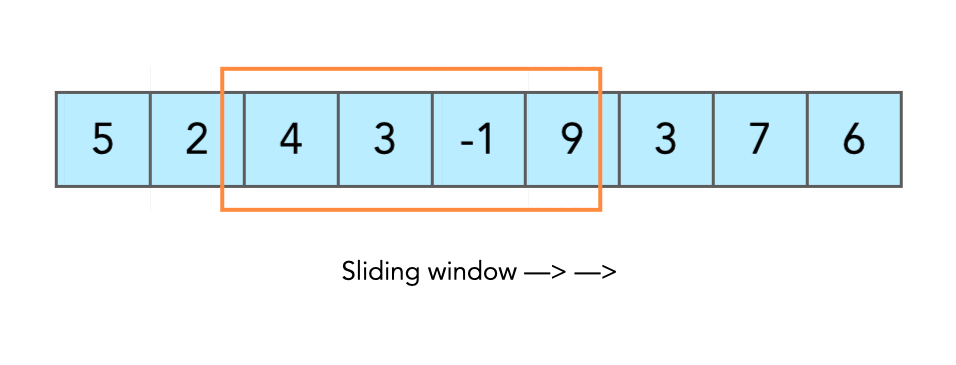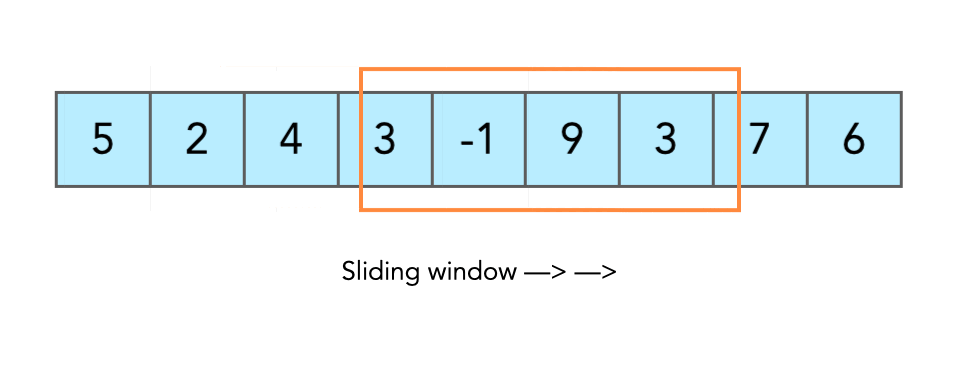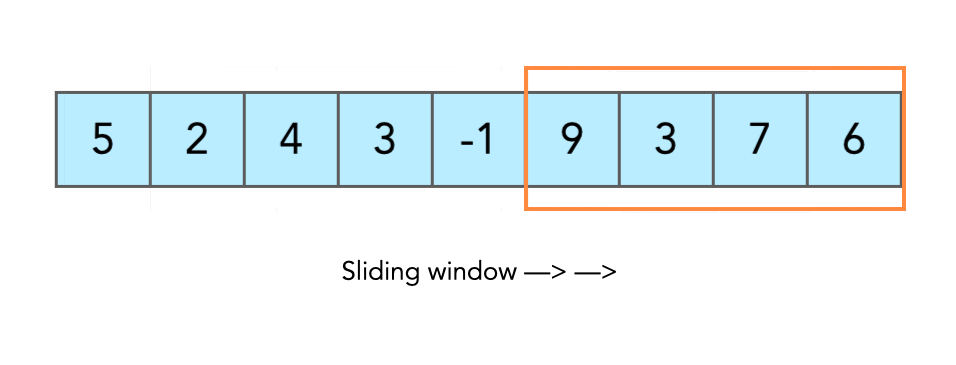
範例題 (1)：MaxSum

來看看這一個很常出現的考題「找最大加總」，就很適合使用 Sliding Window 的邏輯去解，在一個特定 Array 中尋找數個鄰近數字相加的最大值，以下題為例，若要找三數相加最大值，那我們會從 [1,3,5]、[3,5,7]、[5,7,9]…以此類推的方式去做相加，並不斷尋找最大值，那這裡的滑動視窗尺寸就是 3。

const arr = [1, 3, 5, 7, 9, 11, -13, 15, 17, -11];

const MaxSum = (arr, size) => {
    let maxValue = -Infinity;

    if (size > arr.length) {
        return null;
    }

    for (let i = 0; i <= arr.length - size; i++) {
        let attempt = 0;

        for (let j = i; j < i + size; j++) {
            attempt += arr[j];
        }

        if (attempt > maxValue) {
            maxValue = attempt;
        }
    }
    return maxValue;
};

// 27
MaxSum(arr, 3);

// 32
MaxSum(arr, 2);

const BetterMaxSum = (arr, size) => {
    if (size > arr.length) {
        return null;
    }

    let maxValue = 0;
    for (let i = 0; i < size; i++) {
        maxValue += arr[i];
    }

    let tempValue = maxValue;
    for (let j = size; j < arr.length; j++) {
        tempValue = tempValue + arr[j] - arr[j - size];
        if (tempValue > maxValue) {
            maxValue = tempValue;
        }
    }

    return maxValue;
};

BetterMaxSum(arr, 3);

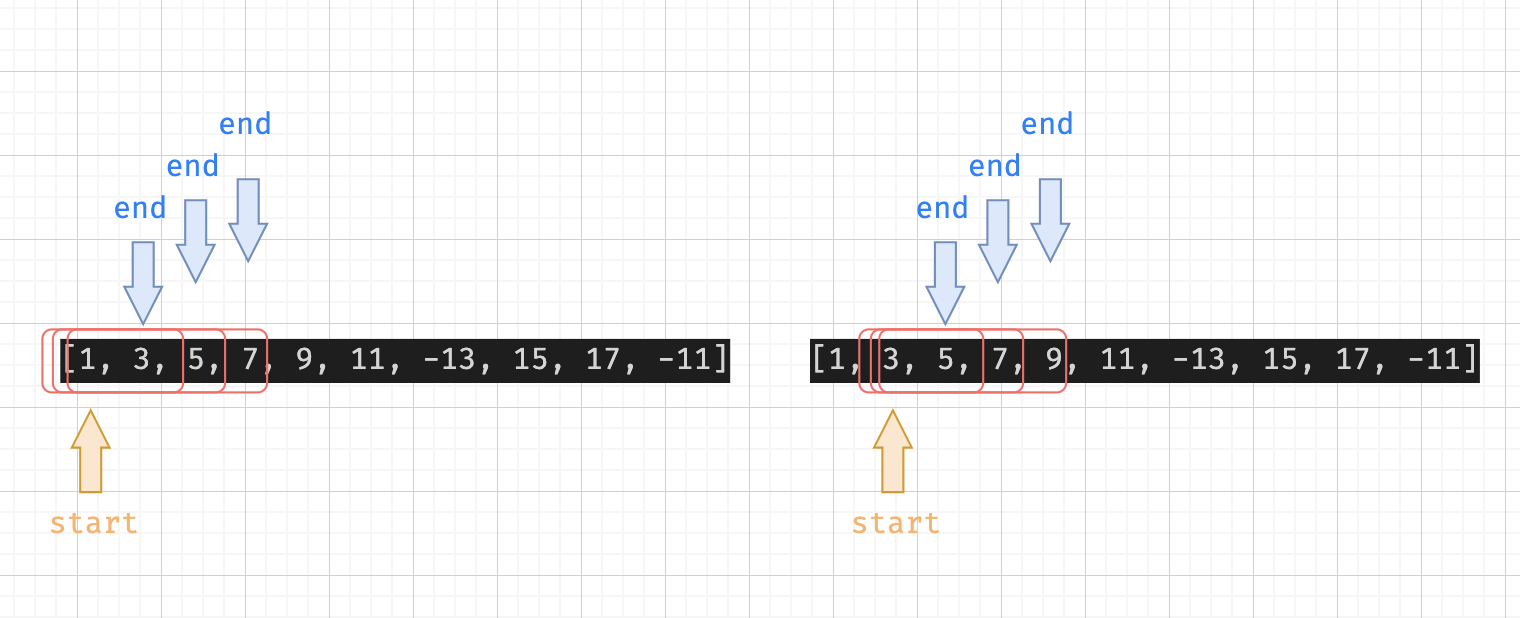
範例題 (2)：MinSubArray

這一題也是陣列題，在一個陣列尋找任一段子陣列，該子陣列數值加總等於題目所求，且子陣列越短越好。這題比較特別的是因為沒有規定加總的子陣列長度，因此此題的視窗端點會是動態變化的，用到了 two pointer 的演算概念。

如圖，給一個 start 與 end，並持續移動 end 值到找到能夠符合目標的總和，若有著接移動 start 試著尋找更短的答案。

const arr = [1, 3, 5, 7, 9, 11, -13, 15, 17, -11];

const MinSubArray = (arr, sum) => {
    let start = 0;
    let end = 0;
    let total = 0;
    let minLength = Infinity;

    while (start < arr.length) {
        if (total < sum && end < arr.length) {
            total += arr[end];
            end++;
        } else if (total >= sum) {
            let currentLength = end - start;
            if (minLength > currentLength) {
                minLength = currentLength;
            }
            total -= arr[start];
            start++;
        } else if (end >= arr.length) {
            break;
        }
    }

    if (minLength === Infinity) {
        console.log("can't find the array!");
        return -1;
    } else {
        console.log(minLength);
        return minLength;
    }
};

MinSubArray(arr, 20);

Recursion 遞迴演算法

1. A function that calls itself
2. Using a data structure called stack. When we are calling a function inside another function, we are on the call stack

遞迴演算法的重要概念有以上兩個要點，一是他是一個被自己呼叫的函式，不斷重複著本身的函式，直到符合條件跳出迴圈。二是我們之所以能使用遞迴是應用函式堆疊 (stack) 的資料結構，stack 這個資料結構本身具有「先進後出」的特性，而遞迴也是會等到一個函式跑完之後再去執行下一次呼叫自己的函式。

了解完遞迴特性，講師 Wilson 以這個數學題目來表達遞迴的運算過程，if (n === 1) 是跳出迴圈的條件，只要 n 為 1，就不會再呼叫本身的函式，但當 n 不為 1 時則會不斷地呼叫自己本身的函式。

也因此下方這段程式碼，雖然只呼叫了 Recursion(3)，但背後其實依序執行了 Recursion(3) => Recursion(2) => Recursion(1)。這也就符合遞迴演算法的「自己呼叫自己直到符合條件跳出迴圈」的要點。

const Recursion = (n) => {
    if (n === 1) {
        return 10;
    } else {
        return Recursion(n - 1) + 15;
    }
};

// Ans: 40 
Recursion(3);

範例題 (1) Fibonacci Sequence

遞迴的範例一是很經典的「斐波那契數列」考題就是運用遞迴的函式，斐波那契數列的函式如下：
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2)

const F(n) => {
    if (n === 0){
        return 0;
    } else if (n === 1){
        return 1;
    } else {
        return F(n - 1) + F(n - 2);
    }
}


// 試算 
for (let i = 0; i < 10; i++){
    console.log(F(i))
}
// Ans: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34

範例題 (2) Array of Arrays

Array of Arrays 一樣是運用了遞迴的演算邏輯，題目給了一個包很多層長得很醜的 Array，目標是把它攤平成一個 Array，這題跳出迴圈的邏輯就是「當不再是 Array 時就結束」。

let uglyArr = [[1, 2], 3, 4, [4, [5]]];
let result = [];
const flattenArr = (uglyArr) => {
    flatter(uglyArr);
    return result;
};

const flatter = (arr) => {
    for (let i = 0; i < arr.length; i++) {
        // 如果還是 Array 則繼續丟進 flatter 繼續拆解
        if (Array.isArray(arr[i])) {
            flatter(arr[i]);
        } else {
            // 如果已經不是 Array 則推 result 這個攤平的 Array 中
            result.push(arr[i]);
        }
    }
};

// Ans: [ 1, 2, 3, 4, 4, 5 ]
flattenArr(uglyArr);

以上就是常見演算法 Sliding Window 與 Recursion 的筆記囉！之後若有機會會再針對 Sorting Algorithm 排序演算法的內容跟大家分享，兩隻腳一起跨進演算法的世界吧～