【筆記】Master the Coding Interview (1) - BigO 時間複雜度

最近在惡補自己的資料結構與演算法，於是選了這門 Andrei Neagoie（以下簡稱 A 大）的課程：Master the Coding Interview: Data Structures + Algorithms，對於非本科生來說也不會太艱深，但光是上課怕自己很容易拋諸腦後，決定把自己的重點消化後整理成 Master the Coding Interview 系列筆記。

這篇的重點是認識 BigO，第一次聽到 BigO 的概念是在 Leetcode 刷題時，發現怎麼提交怎麼超時，近一步去了解才知道基本上使用雙層迴圈就是時間複雜度 O(n^2)，也就是計算花費時間過多的情況在 Leetcode 考題中的會被拒絕提交。也因此許多看似雙迴圈比對（同事都稱他為暴力解）就能解的考題其實都在考該如何把時間複雜度控制在 O(n) 或是 O(Log n)。

為什麼我們要認識 Big O 時間複雜度？

首先 A 大先拋出一個直球，問了 What is good code？

Readable：可讀性佳，也就是很好閱讀與維護的程式碼，常常聽到 Clean Code、Coding Style Consistent 等都屬於這項
Scalable：可規模化，意思是你的程式在資料量大時還能夠在可接受的時間與容量限制下運作。沒錯 Scalable 又可以細分為 Speed 與 Memory

Memory 就是空間複雜度，而 Speed 則是呼應時間複雜度。在時間複雜度中我們會用 BigO 這樣的符號來表示其層級，其實時間複雜度背後代表的意義不是該函式所花費的時間，而是語法執行的次數，只是花費的時間與演算法中的執行次數成正比，因此我們會用花費時間來思考。

認識幾個常見的 Big O

1. O(n) Linear Time
runTime 由 n 決定，我們常用的 for loop 就是這個情境，隨著輸入的值越多，執行的次數也會成正比的增長

2. O(1) Constant Time
一次只做一件事，因此他會是一條平行的線

3. O(n^2)
雙層 for loop 情境，Leetcode 許多考題都在解決 O(n^2) 的時間複雜度

4. O(!n)
n 階，Nested loop with all inputs，基本上出現這個情境就是砍掉重寫，所以叫做 OhNo

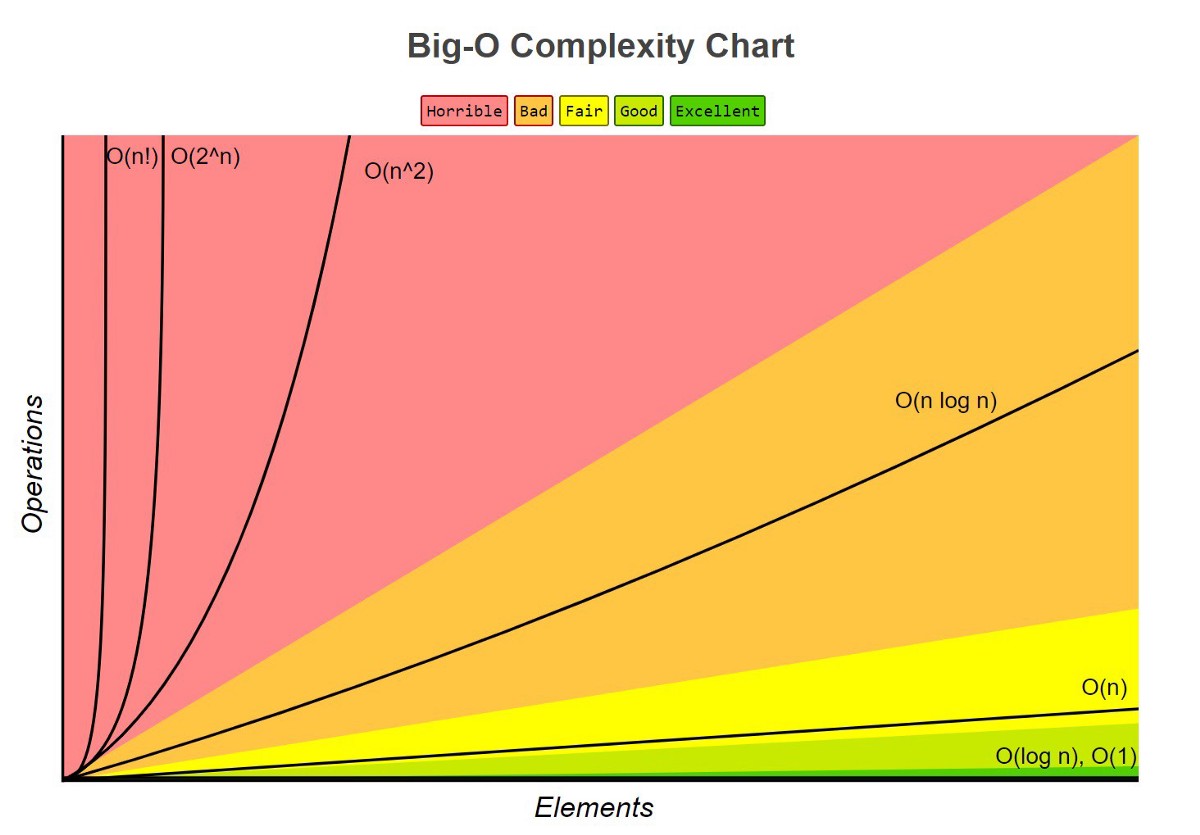
這張圖是很經典的時間複雜度比較圖，把所有的時間複雜度的情況都畫了出來，X 軸 Elements 是 Input 到函式中的數值，y 軸 Operations 就是該函式執行的次數，隨著數值增加一直到接近無限大時，所對應的執行次數會維持、遞增甚至指數成長。

BigO
Image Source

影響函式運算時間的幾個要素

只要掌握這幾個要素，也能讓自己的程式碼運算速度提升，但是其實現在的電腦效能都很好，除非資料量大不然其實很難察覺到毫秒之間的差異。

Operation 賦值運算子（+ - * /）
Comparisons 比較運算子 (> < = )
Looping 迴圈（for, while）
Outside Function Call func(func(func()))

掌握時間複雜度的 4 守則

1. Worst Case

永遠都要思考最糟的情況，例如在 Array 裡找數值，結果 Array 的最後一個值才是我們要的數值，那就代表有 n 個值就要跑 n 次。

1
2
3
4
5
6
7
8
9

const Zoo = [bear, giraffe, elephant, pig, monkey]

const findMonkey = () => {
    Zoo.find( item => 
        item === "monkey"
    )
}

2. Remove Constant
不論在函式內宣告多少個常數，常數都是可以被忽略的。

3. Different Terms of Input
注意輸入函式的 Inputs，若有 K 個 Inputs 分別去跑 for loop，那時間複雜度就「不會」是 O(Kn) 而是 O(A + B)。

1 2	arrayA.forEach(()=>{}) arrayB.forEach(()=>{})

4. Drop Non Dominants
忽略非主要控制的函式，哈翻成中文好奇怪～簡單來說就是直接取複雜度最高的情境，其他都可以被省略。例如：O(n + n^2) 可以直接視為 O(n^2)。

// O(n)
arrayA.forEach(()=>{});

// O(n^2)
arrayB.forEach((number) => {
    number.forEach(()=>{});
})

以上就是 A 大在 Big O 單元中提到的幾個重點，加上查了一些資料的補充，大家有想法都可以再跟我分享唷！繼續去上課囉～